Answer:
You will receive $201.38 more interest if the investment is made with a compound interest rate rather than a simple interest rate.
Step-by-step explanation:
Simple interest rate
We can calculate how much interests you'd obtain if you deposited the $2,600 in a simple interest rate account.
We start using the following formula for calculating the simple interests:
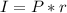
Where:
I are the interests per year,
P is the amount being invested,
r is the interest rate.
Replacing in the formula with the given values we have:
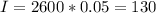
We then proceed to multiply this result by the given number of years, which is 8. We get
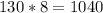 .
.
Finishing with the simple interest rate, if we wanted to know how much is the investment worth at the end of a 8 year period, we must merely add the principal (the $2,600) to the total interests after the end of the period ($1040). So
 .
.
We'll use these results later.
Compound interest rate
The formula for compound interests is the following:
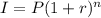
Where:
I is the value of the investment after n years,
P is the principal amount being invested,
r is the interest rate,
n are the number of years the investment is compounded.
Replacing in the formula with the given values we have:
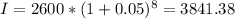
After the 8 year period, the investor will have $3841.38 in it's compounded interest account.
Comparing these results
We can simply substract the value of both investments at the end of a 8 year period, to determine how much more interest does the compound interest rate account give in relation to a simple interest rate account.
The values we've gotten were:
$3,640 for the simple interest rate account, and
$3,841.38 for the compounded interest rate account.
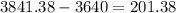 . Therefore the answer is: the account that pays compounded interests will pay $201.38 more to this invididual, compared to an account that pays simple interest.
. Therefore the answer is: the account that pays compounded interests will pay $201.38 more to this invididual, compared to an account that pays simple interest.