Step-by-step explanation:
The standard reduction potential
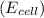 is given as 1.27 V.
is given as 1.27 V.
Concentration of
 = 1.0 M
= 1.0 M
Hence, reduction reaction is as follows.

Oxidation reaction is as follows.

Therefore, overall net chemical equation will be as follows.
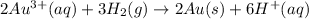
As, its is known that standard electrode potential (
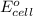 ) for hydrogen is equal to zero.
) for hydrogen is equal to zero.
And, standard electrode potential for
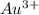 is
is
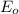 equal 1.50 V.
equal 1.50 V.
Hence, formula to calculate standard cell potential is as follows.
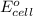 =
=
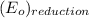 -
-
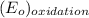
= 1.50 V - 0 V
= 1.50 V
Therefore, concentration of
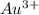 is calculated as follows.
is calculated as follows.
![E_(cell) = E^(o)_(cell) - (0.059)/(2)log ([H^(+)]^(6))/([Au^(3+)]^(2))](https://img.qammunity.org/2020/formulas/chemistry/college/v8bkz7692dx14i3qwqimw84ce8pqg9ztp5.png)
Hence, substitute the given values as follows.
![E_(cell) = E^(o)_(cell) - (0.059)/(2)log ([H^(+)]^(6))/([Au^(3+)]^(2))](https://img.qammunity.org/2020/formulas/chemistry/college/v8bkz7692dx14i3qwqimw84ce8pqg9ztp5.png)
1.27 = 1.50 - \frac{0.059}{6}log \frac{(1)^{6}}{[Au^{3+}]^{2}}[/tex]
![log(1)/([Au^(3+)]^(2))](https://img.qammunity.org/2020/formulas/chemistry/college/ceuv247o3n7g4u0o1kyuu365xhgqugp3e4.png) = 23
= 23
Taking antilog on both the sides, the above equation will be as follows.
![(1)/([Au^(3+)]^(2))](https://img.qammunity.org/2020/formulas/chemistry/college/8ktj785srsxjevacfin016rlp2mx94z1xn.png) =
=
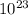
=
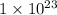
![(1)/([Au^(3+)]^(2))](https://img.qammunity.org/2020/formulas/chemistry/college/8ktj785srsxjevacfin016rlp2mx94z1xn.png) =
=
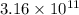
![[Au^(3+)]](https://img.qammunity.org/2020/formulas/chemistry/college/ej3a12jmelzr6zttlce27raa00t8np7rmp.png) =
=
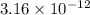 M
M
Hence, we can conclude that the concentration for
![[Au^(3+)]](https://img.qammunity.org/2020/formulas/chemistry/college/ej3a12jmelzr6zttlce27raa00t8np7rmp.png) is
is
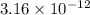 M.
M.