Answer:
$584.88
Explanation:
If $396 is invested at an interest rate of 13% per year and is compounded continuously in 3 years.
Formula of continuous compound interest :
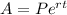
Where
A = Future Amount
P = Principal amount ( $396.00 )
r = rate of interest 13% ( 0.13 )
t = time in years (3 years)
Now put the values in the formula
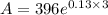
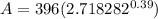
= 396 (1.476981)
= 584.884394 ≈ 584.88
The amount after 3 years would be $584.88