Question

A long, thin solenoid has 950 turns per meter and radius 3.00 cm. The current in the solenoid is increasing at a uniform rate of 63.0 A>s. What is the magnitude of the induced electric field at a point near the center of the solenoid and (a) 0.500 cm from the axis of the solenoid; (b) 1.00 cm from the axis of the solenoid?

Answer 1

Part a)

`E = 0.188 * 10^(-3) N/C</p><p>Part b)</p><p>[tex]E = 0.376 * 10^(-3)`N/C

Step-by-step explanation:

As we know that the magnetic field near the center of the solenoid is given as

`B = \mu_0 ni`

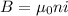
Also we know by equation of Faraday's law

EMF induced in the closed loop will be equal to rate of change in magnetic flux

so we have

`EMF = A(dB)/(dt)`

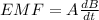
so we have

`\int E. dL = \pi r^2 (\mu_0 n (di)/(dt))`

`E. (2\pi r) = \pi r^2 (\mu_0 n (di)/(dt))`

`E = (\mu_0 n r)/(2) (di)/(dt)`

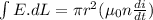
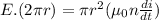
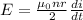
Part a)

At r = 0.500 cm

we have

`E = (4\pi * 10^(-7) (950) (0.500 * 10^(-2)))/(2)(63)`

`E = 0.188 * 10^(-3) N/C`

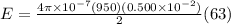
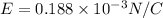
Part b)

At r = 1.00 cm

we have

`E = (4\pi * 10^(-7) (950) (1.00 * 10^(-2)))/(2)(63)`

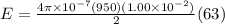
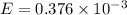`E = 0.376 * 10^(-3)`N/C