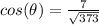Question

HELP ASAP!!! Suppose θ is an angle in the standard position whose terminal side is in Quadrant IV and cotθ = -7\18

Find the exact values of the five remaining trigonometric functions of θ.

Answer 1

The answer is the third option

Part 1)
`csc(\theta)=-(√(373))/(18)`

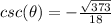
Part 2)
`sin(\theta)=-(18)/(√(373))`

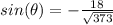
Part 3)
`tan(\theta)=-(18)/(7)`

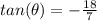
Part 4)
`sec(\theta)=(√(373))/(7)`

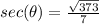
Part 5)
`cos(\theta)=(7)/(√(373))`

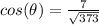
Explanation:

we know that

If angle theta lie on Quadrant IV

then

The function sine is negative

The function cosine is positive

The function tangent is negative

The function secant is positive

The function cosecant is negative

step 1

Find
`csc(\theta)`

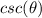
we know that

`cot^(2) (\theta)+1=csc^(2) (\theta)`

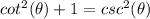
we have

`cot(\theta)=-(7)/(18)`

substitute

`(-(7)/(18))^(2)+1=csc^(2) (\theta)`

`(49)/(324)+1=csc^(2) (\theta)`

`(373)/(324)=csc^(2) (\theta)`

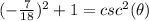
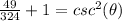
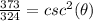
square root both sides

`csc(\theta)=-(√(373))/(18)`

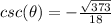
step 2

Find
`sin(\theta)`

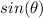
we know that

`csc(\theta)=(1)/(sin(\theta))`

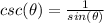
we have

`csc(\theta)=-(√(373))/(18)`

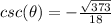
therefore

`sin(\theta)=-(18)/(√(373))`

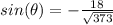
step 3

Find
`tan(\theta)`

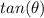
we know that

`tan(\theta)=(1)/(cot(\theta))`

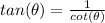
we have

`cot(\theta)=-(7)/(18)`

therefore

`tan(\theta)=-(18)/(7)`

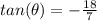
step 4

Find
`sec(\theta)`

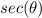
we know that

`tan^(2) (\theta)+1=sec^(2) (\theta)`

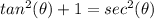
we have

`tan(\theta)=-(18)/(7)`

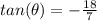
substitute

`(-(18)/(7))^(2)+1=sec^(2) (\theta)`

`(324)/(49)+1=sec^(2) (\theta)`

`(373)/(49)=sec^(2) (\theta)`

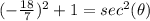
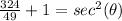
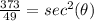
square root both sides

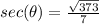`sec(\theta)=(√(373))/(7)` -----> is positive

step 5

Find
`cos(\theta)`

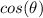
we know that

`sec(\theta)=(1)/(cos(\theta))`

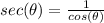
we have

`sec(\theta)=(√(373))/(7)`

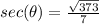
therefore

`cos(\theta)=(7)/(√(373))`