Answer:
The difference in atomic mass between the two isotopes is 1.00452329 atomic mass unit.
Step-by-step explanation:
For an isotope-I (heavier)
Mass of an isotope-I=M
Number of neutrons = n+1
Number of protons = p
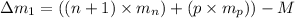
For an isotope-II
Mass of an isotope-II=M'
Number of neutrons = n
Number of protons = p
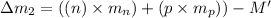
Difference in binding energy:
 (general binding energy expression)
(general binding energy expression)
Binding energy difference between two isotopes:
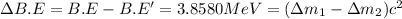 ..(1)
..(1)
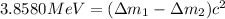
![=([((n+1)* m_n)+(p* m_p))-M]-[((n)* m_n)+(p* m_p))-M'])c^2](https://img.qammunity.org/2020/formulas/chemistry/college/e1y71zzmcnjqph72qr8eaaq2ms82q0s6vi.png)
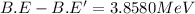
![=([((n+1)* m_n)+(p* m_p))-M]-[((n)* m_n)+(p* m_p))-M'])c^2](https://img.qammunity.org/2020/formulas/chemistry/college/e1y71zzmcnjqph72qr8eaaq2ms82q0s6vi.png)
![3.8580 MeV=[1* m_n-M+M']c^2](https://img.qammunity.org/2020/formulas/chemistry/college/r204ml49xt4qm468wve6au0qxus0bnjok4.png)

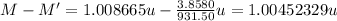
The difference in atomic mass between the two isotopes is 1.00452329 atomic mass unit.