Answer:

Explanation:
Let
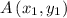 and
and
 be two points then distance AB is equal to
be two points then distance AB is equal to
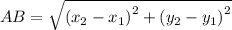
Here, a curve is traced by a point
 which moves such that its distance from the point
which moves such that its distance from the point
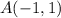 is three times its distance from the point
is three times its distance from the point
 i.e
i.e

Using distance formula,
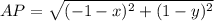
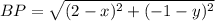
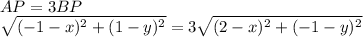
On squaring both sides, we get
![(-1-x)^2+(1-y)^2=9\left [ (2-x)^2+(-1-y)^2 \right ]\\1+x^2+2x+1+y^2-2y=9\left ( 4 +x^2-4x+1+y^2+2y\right )\\1+x^2+2x+1+y^2-2y=36+9x^2-36x+9+9y^2+18y\\8x^2+8y^2+43-38x+20y=0](https://img.qammunity.org/2020/formulas/mathematics/high-school/94q77lj6759nrsvwgrtzehbyf4aorem3iu.png)
So, equation of curve is
