Question

You have determined the critical path in a CPM analysis. You would like to determine the probability of completing the project is a desired period of time. One of the activities on the critical path has an optimistic time of 5 minutes, a most likely time of 6, and a pessimistic time of 17. What is the variance estimate of this activity?

Answer 1

The variance estimate of this activity is 4.

Explanation:

Given information: One of the activities on the critical path has

Optimistic time = 5 minutes

Most likely time = 6 minutes

Pessimistic time = 17 minutes

The variance estimate of a activity is

`\sigma ^2=((t_p-t_o)/(6))^2`

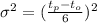
where,
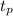`t_p` is pessimistic time of that activity and
`t_o` is optimistic time of that activity.

The variance estimate of the given activity is

`\sigma ^2=((17-5)/(6))^2`

`\sigma ^2=((12)/(6))^2`

`\sigma ^2=2^2`

`\sigma ^2=4`

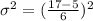
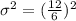
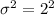
Therefore the variance estimate of this activity is 4.