Answer:
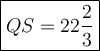
Explanation:
Look at the picture.
We must start from domain:
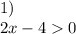 add 4 to both sides
add 4 to both sides
 divide both sides by 2
divide both sides by 2
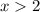
and
 add 1 to both sides
add 1 to both sides
 divide both sides by 4
divide both sides by 4
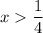
and
 add 43 to both sides
add 43 to both sides
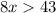 divide both sides by 8
divide both sides by 8
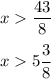
From 1, 2 and 3 we have:
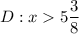
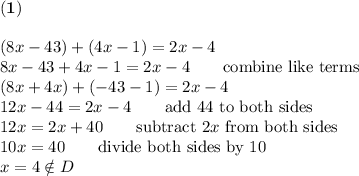

R is midpoint of QS. Therefore QR = RS ⇒ QS = 2(RS).
RS = 2x - 4
Put the value of x and calculate the length of RS:

Therefore
