Answer:
46
Explanation:
Let
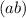 represent a number with
represent a number with
 in the ten's position and
in the ten's position and
 is the one's position.
is the one's position.
This means
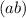 actually has value of
actually has value of
 .
.
We are given the sum of those digits of
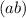 is 10; this means
is 10; this means
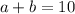 .
.
It says if 18 is added to the number
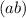 , then the result is
, then the result is
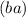 .
.
So
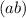 has value
has value
 and
and
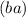 has value
has value
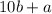 .
.
We are given then:
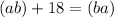
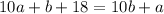
Subtract
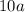 on both sides:
on both sides:
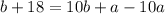
Simplify:

Subtract
 on both sides:
on both sides:
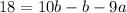
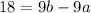
Divide both sides by 9:
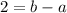
Rearrange by commutative property:
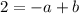
So the system of equations we want to solve is:
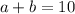
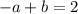
-------------------------Add equations together (this will eliminate the variable
 and allow you to go ahead and solve for
and allow you to go ahead and solve for
 :
:

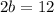
Divide both sides by 2:
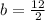
Simplify:
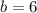
If
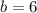 and
and
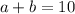 , then
, then
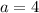 .
.
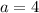 since 4+6=10.
since 4+6=10.
So the original number is (46).
18 more than 46 is 18+46=(64) which is what we wanted.
We also have the sum of 4 and 6 is 10 as well.