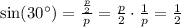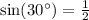Question

Show that sin (30°) = 1/2

Answer 1

Geometric proof in explanation.

Explanation:

Draw an equilateral triangle.

A equilateral triangle has it's sides all congruent and all it's angles measures 60 degrees.

We are going to draw a line segment to cut the equilateral triangles into two congruent right triangles. I will do this in the attachment with p being positive.

You can see we will get 30-60-90 triangles.

We don't need to find the adjacent measurement to the angle whose measurement is 30 degrees since sine is opposite over hypotenuse.

`\sin(30^\circ)=((p)/(2))/(p)=(p)/(2) \cdot (1)/(p)=(1)/(2)`

`\sin(30^\circ)=(1)/(2)`