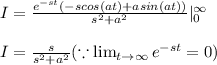Answer:
We have laplace transform of any function is defined as
![L[{f(t)}]=\int_(0)^(\infty )f(t)e^(-st)dt](https://img.qammunity.org/2020/formulas/mathematics/college/a1ujr8x1wr99i1n70gsjg14lbaf327103x.png)
thus for
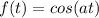
![L[cos(at)]=\int_(0)^(\infty )cos(at)e^(-st)dt](https://img.qammunity.org/2020/formulas/mathematics/college/drjo1natod6cg7bftnrw63kbro2iweo6tm.png)
Now integrating the given expression using the integration by parts principle we have
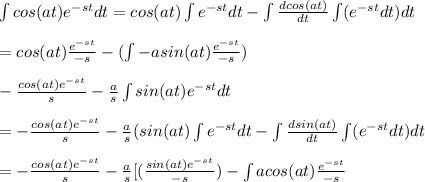
Note that we get the first integral back in the RHS expression
Thus solving we have
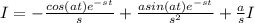
Solving for I we get
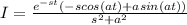
now applying the limits we have