Question

A four​-digit number starts with a number between 5​-9 in the first​ position, with no restrictions on the remaining 3 digits. a right parenthesis Find the probability that a​ randomly-chosen phone number contains all different digits. b right parenthesis Find the probability that a​ randomly-chosen phone number contains at least one repeated digit.

Answer 1

a. 0.504

b. 0.496

Explanation:

Given,

There are 4 digit in a number,

In which the possible number in first position = 3 (i.e. 6, 7, 8 )

If the repetition of digit is not allowed,

The possible number in second position = 9

In third position = 8

And, in fourth position = 7

Thus, the possible ways of arranging a number in which each contains different digit

= 3 × 9 × 8 × 7

= 1512,

While, the total possible ways of arranging 4 numbers = 3 × 10 × 10 × 10 = 3000

a. Hence, the probability that a​ randomly-chosen phone number contains all different digits =
`(1512)/(3000)`

`=0.504`

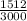
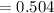
b. The probability that a​ randomly-chosen phone number contains at least one repeated digit = 1 - the probability that a​ randomly-chosen phone number contains all different digits

= 1 - 0.504

= 0.496