Answer:
The volume of solid will be
 cubic unit
cubic unit
Explanation:
Given: The given curves

Rotation about y-axis to form a solid bounded by given curve, x=2 and y=0.
Please see the attachment for figure.
Volume of solid rotation about y-axis using cylindrical shell method.
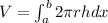
where,
a is lower limit (a=0)
b is upper limit (b=2)
r is radius (r=x)
h is height (
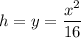 )
)
using the above formula the volume of solid we get
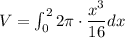
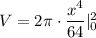
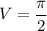
Hence, The volume of solid will be
