Question

Waves from a radio station have a wavelength of 220 m. They travel by two paths to a home receiver 20.0 km from the transmitter. One path is a direct path, and the second is by reflection from a mountain directly behind the home receiver. What is the minimum distance from the mountain to the receiver that produces destructive interference at the receiver

Answer 1

`x_(min) = 55`

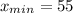
Given:

wavelength,
`\lambda` = 220 m

distance from reciever = 20 km

Solution:

To calculate the path difference in case of the destructive interference:

path difference,
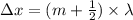`\Delta x = (m + (1)/(2))* \lambda` (1)

where m = 0, 1, 2, 3.....

here, m = 0

Therefore, eqn (1) is reduced to:

`\Delta x = (0 + (1)/(2))*\lambda= (\lambda )/(2) = (220)/(2) = 110 m`

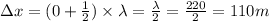
Now, the minimum distance
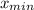`x_(min)` from mountain to reciever to generate destructive interference at the reciever:

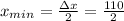`x_(min) = (\Delta x)/(2) = (110)/(2)` = 55 m