Answer:
The lines are perpendicular
Explanation:
For a couple of points
 and
and
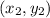 the formula to calculate the slope of a line is:
the formula to calculate the slope of a line is:

If two lines are parallel then their slopes are equal, but if two lines of slopes
 and
and
 are perpendicular then it is true that:
are perpendicular then it is true that:
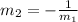
For the points (–6, –1) and (–11, 1) the slope of the line is:

For the points (–3, –8) and (–5, –13) the slope of the line is:
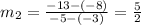
Note that
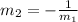
So the lines are perpendicular