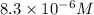Question

A 25.00-mL sample of propionic acid, HC3H5O2, of unknown concentration was titrated with 0.141 M KOH. The equivalence point was reached when 43.76 mL of base had been added. What is the hydroxide-ion concentration at the equivalence point? Ka for propionic acid is 1.3 × 10–5 at 25°C. a. 1.5 × 10-9 M b. 1.1 × 10-3 M c. 1.1 × 10-5 M d. 8.3 × 10-6 M e. 1.0 × 10-7 M

Answer 1

Concentration of hydroxide-ion at equivalence point =
`8.3* 10^(-6)M`

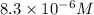
Step-by-step explanation:

`HC_(3)H_(5)O_(2)+KOH\rightarrow C_(3)H_(5)O_(2)^(-)K^(+)+H_(2)O`

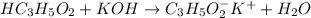
1 mol of
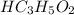`HC_(3)H_(5)O_(2)` reacts with 1 mol of KOH to produce 1 mol of
`C_(3)H_(5)O_(2)^(-)`

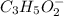
At equivalence point, all
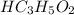`HC_(3)H_(5)O_(2)` gets converted to
`C_(3)H_(5)O_(2)^(-)`.

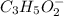Moles of
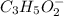`C_(3)H_(5)O_(2)^(-)` produced at equivalence point is equal to moles of KOH added to reach equivalence point.

So, moles of
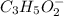`C_(3)H_(5)O_(2)^(-)` produced =
`(43.76* 0.141)/(1000)moles=0.00617moles`

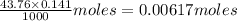
Total volume of solution at equivalence point = (25.00+43.76) mL = 68.76 mL

Concentration of
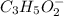`C_(3)H_(5)O_(2)^(-)` at equivalence point =
`(0.00617* 1000)/(68.76)M=0.0897M`

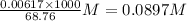
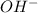`OH^(-)` produced at equivalence point is due to hydrolysis of
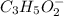`C_(3)H_(5)O_(2)^(-)`. We have to construct an ICE table to calculate concentration of
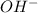`OH^(-)` at equivalence point.

`C_(3)H_(5)O_{}^(-)+H_(2)O\rightleftharpoons HC_(3)H_(5)O_(2)+OH^(-)`

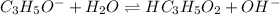
I:0.0897 0 0

C: -x +x +x

E: 0.0897-x x x

`([HC_(3)H_(5)O_(2)][OH^(-)])/([C_(3)H_(5)O_(2)^(-)])=K_(b)(C_(3)H_(5)O_(2)^(-))=(10^(-14))/(K_(a)(HC_(3)H_(5)O_(2)))`

species inside third bracket represent equilibrium concentrations

So,
`(x^(2))/(0.0897-x)=7.69* 10^(-10)`

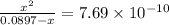
or,
`x^(2)+(7.69* 10^(-10)* x)-(6.90* 10^(-11))=0`

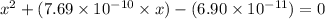
So,
`x=\frac{-(7.69* 10^(-10))+\sqrt{(7.69* 10^(-10))^(2)+(4* 6.90* 10^(-11))}}{2}`M =
`8.3* 10^(-6)M`

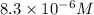
So, concentration of hydroxide-ion at equivalence point = x M =
`8.3* 10^(-6)M`