Question

To compare the popularity rates of two different political candidates in their respective states, a random sample of 212 citizens from State A yielded 145 who were in favor of their state's candidate whereas 128 citizens out of the 200 selected from State B were in favor of their state's candidate. We wish to use a significance level of 0.05 to test whether there exists a difference between the popularity rates of these two candidates.

Answer 1

There exists no difference between the popularity rates of these two candidates.

Explanation:

Given : a random sample of 212 citizens from State A yielded 145 who were in favor of their state's candidate whereas 128 citizens out of the 200 selected from State B were in favor of their state's candidate.

To Find : We wish to use a significance level of 0.05 to test whether there exists a difference between the popularity rates of these two candidates.

Solution:

A random sample of 212 citizens from State A yielded 145 who were in favor of their state's candidate

So,
`n_1=212, y_1=145`

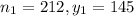
128 citizens out of the 200 selected from State B were in favor of their state's candidate.

`n_2=200, y_2=128`

We will use Comparing Two Proportions

`\widehat{p_1}=(y_1)/(n_1)`

`\widehat{p_1}=(145)/(212)`

`\widehat{p_1}=0.68`

`\widehat{p_2}=(y_2)/(n_2)`

`\widehat{p_2}=(128)/(200)`

`\widehat{p_2}=0.64`

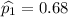
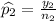
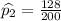
Let p_1 and p_2 be the probabilities of the popularity rates of these two candidates.

`H_0:p_1=p_2\\H_a:p_1\\eqp_2`

`\widehat{p}=(y_1+y_2)/(n_1+n_2) =(145+128)/(212+200)=0.66`

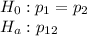
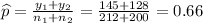
Formula of test statistic :
`\frac{\widehat{p_1}-\widehat{p_2}}{\sqrt{\widehat{p}(1-\widehat{p})((1)/(n_1)+(1)/(n_2))}}`

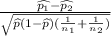
Substitute the values

test statistic :
`\frac{0.68-0.64}{\sqrt{0.66(1-0.66)((1)/(212)+(1)/(200))}}`

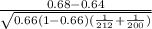
test statistic : 0.856

refer z table for p value

p value = 0.8023

α = 0.05

Since p value >α

So, we accept the null hypothesis

Hence there exists no difference between the popularity rates of these two candidates.