Question

A building needs a ramp to make it handicap accessible. By law, the ramp must run 10 inches horizontally for every 1 inch of rise. If the surface of the ramp is 57 inches long how far above the ground is the inclined end of the ramp? Round to the nearest tenth of an inch.

Answer 1

Inclined ramp will be 5.7 inches above the ground.

Explanation:

A building needs a ramp to make it handicap accessible.

Law says, "the ram must run 10 inches horizontally for every 1 inch rise".

In the figure attached, ramp is given with a horizontal length 10 inches and vertical rise 1 inch.

Length of hypotenuse of the right triangle =
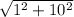`\sqrt{1^(2)+10^(2)}` [By Pythagoras theorem]

=
`√(1+100)`

=
`√(101)`

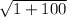
Now a second ramp is given which is similar to the previous one with the hypotenuse 57 inches and we have to calculate the vertical length.

By the property of similar triangles - "All corresponding sides will be in the same ratio"

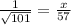
`(1)/(√(101))=(x)/(57)`

x =
`(57)/(√(101) )`

=
`(57)/(10.05)`

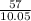
= 5.67 inches

≈ 5.7 inches

Answer 2

The inclined end of the ramp is 5.7 in above the ground

Explanation:

step 1

we know that

The ramp must run 10 inches horizontally for every 1 inch of rise

Applying the Pythagoras Theorem, find the hypotenuse

`d^(2)=10^(2)+1^(2)`

`d^(2)=101`

`d=√(101)\ in`

step 2

Using proportion find out the height of the ramp

Let

x ----> the height of the ramp

`(x)/(57)=(1)/(√(101)) \\ \\x=(57)/(√(101))\\ \\x=5.7\ in`