Question

3. The average annual income of 100 randomly chosen residents of Santa Cruz is $45,221 with a standard deviation of $30,450. a. What is the standard deviation of the mean annual income? b. Test the 1-sided hypothesis that the average annual income is $40,000 against the alternative that it is less than $40,000 at the 10% significance level. c. Test the 2-sided hypothesis that the average annual income is equal to $42,000 against the alternative that it is not at the 5% significance level. d. What is the confidence interval for part (c)? e. What is the p-value for part (b)? f. Do you reject or fail to reject part (c)? Please write your answer and a complete, accurate, sentence.

Answer 1

Explanation:

Given that the average annual income of 100 randomly chosen residents of Santa Cruz is $45,221 with a standard deviation of $30,450.

a) Std deviation of mean =
`(\sigma)/(√(n) ) \\=3045`

b)
`H_0: x bar =40000\\H_a: x bar <40000\\\alpha = 10%`

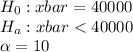
Test statistic = Mean diff/std dev of mean =
`(-5221)/(3045) \\=-1.715`

p value = 0.043

Since p >0.01 we accept null hypothesis.

c) For two sided p value = 0.086

Here we have

`H_0: x bar =42000\\H_a: x bar \\eq 42000\\\alpha = 0.05`

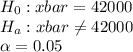
Test statistic =
`(-3000)/(3045) \\\\=-0.99`

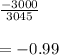
p value = 0.3221

Since p >alpha, we accept null hypothesis.