Question

A study claims that college students spend an average of 4 hours or less studying per day. A researcher wants to check if this claim is true. A random sample of 121 college students randomly selected and it showed that average of hours studying per day was 3.15 with a standard deviation of 1.2 hours. Using the 10% significance level, can you conclude that the claim college students spend an average of 4 hours or less studying per day is valid?

Answer 1

Answer with explanation:

Let
`\mu` be the population mean.

By observing the given information, we have :-

`H_0:\mu\leq4\\\\H_a:\mu>4`

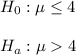
Since the alternative hypotheses is left tailed so the test is a right-tailed test.

We assume that the time spend by students per day is normally distributed.

Given : Sample size : n=121 , since n>30 so we use z-test.

Sample mean :
`\overline{x}=3.15`

Standard deviation :
`\sigma=1.2`

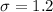
Test statistic for population mean :-

`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

`\Rightarrow\ z=(3.15-4)/((1.2)/(√(121)))\\\\\Rightarrow\ z=-7.79166666667\approx-7.79`

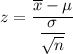
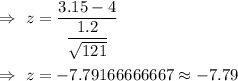
Critical value (one-tailed) corresponds to the given significance level :-

`z_(\alpha)=z_(0.1)=1.2816`

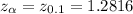
Since the observed value of z (-7.79) is less than the critical value (1.2816) , so we do not reject the null hypothesis.

Hence, we conclude that we have enough evidence to accept that the college students spend an average of 4 hours or less studying per day.