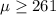Question

An article in a local town newspaper discusses the results of state test scores in their town. The reporter headlines, "The students in this town don't have the necessary skills." The state test says that a score of 261 or higher on its test reflects the student has the skills needed to graduate. A local town newspaper conducted a random sample of 200 students and found the mean to be 257 and a standard deviation of 41 points. Is this sample result good evidence that the mean of all students in this town is less than 261

Answer 1

We are supposed to find Is this sample result good evidence that the mean of all students in this town is less than 261

Sample size = n = 200

`\bar{x}=257`

`\mu = 257`

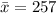
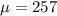
Since n>30

Standard deviation =
`\sigma = 41`

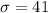
So,we will use z test

`H_0:\mu \geq 261\\H_a:\mu < 261`

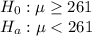
Formula :
`z=\frac{\bar{x}-\mu}{(\sigma)/(√(n))}`

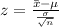
Substitute the values

`z=(257-261)/((41)/(√(200)))`

`z=-1.37`

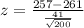
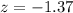
Now find the p value from the z table

P(z<-1.37)=0.0853

Let us suppose the significance level is 5 %

So, α = 0.05

p value > α

So, we accept the null hypothesis
`\mu \geq 261`