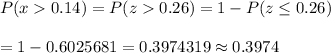Answer: 0.3974
Explanation:
Given : The distribution of annual returns on common stocks is roughly symmetric, so the mean return over even a moderate number of years is close to Normal.
Real annual returns on U.S. common stocks had mean :
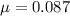
Standard deviation :
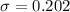
We assume that the past pattern of variation continues.
Let x be the random variable that represents the annual returns on common stocks over the next 32 years .
The formula for z-score :

For x= 0.14,

By using the standard normal distribution table , we have
The probability that the mean annual return on common stocks over the next 32 years will exceed 14% :-