Answer:
The Mean is not equal to $31,129.
Explanation:
Consider the provided information.
The mean is $31129
Thus, the null hypothesis
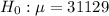
Alternative hypothesis
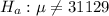
A random sample of 15 firstyear CMAs in Denver produces a mean salary of $32,279, with a standard deviation of $1,797.
Thus the value mean of sample is 32279, standard deviation is 1797 and number of samples are 15.
Now use the 2 sided t-test.
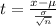
Now substitute the respective values in the above formula.
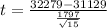
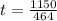
Test Value = 2.4785 approximately
Now, find the corresponding p-value in your t-table with DF(degree of freedom) 14.
p = 0.0265
as the value of p < 0.05, so you reject null hypothesis.
Thus, the Mean is not equal to $31,129.