Answer:
V = 19.42 cubic cm.
Explanation:
The area of the cylindrical packege is

and, its volume is
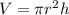
where r is the radius and h is the height.
If $4 is the maximun you can spend and, each square cm cost $0.10 then, the maximun amount of square cm that is available is 40 square cm (by a simple rule of three). So
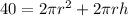
from this we can get that

substituting this in the volume formula leads us to
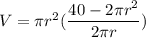
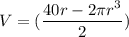
For finding the maximun volume we use derivatives (we know that the maximun volume can be found where its derivative is equal to 0). Since the volume depends of the radius, we have
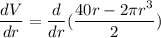
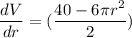
For the value of r that maximizes the volume we have that
 . So
. So
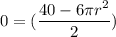
and
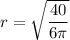 .
.
Now that we have the radius that maximizes the volume, the only thing that is left is to replace it in the volume formula:
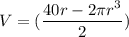
Thus
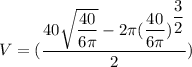
After computing this, we get :
V = 19.42 cubic cm.