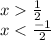1/x<4x (1)/(x) < 4x ​

Question

1/x<4x

`(1)/(x) < 4x`
​

Answer 1

`x>(1)/(2) \\x<(-1)/(2)`

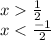
Explanation:

If we solve for 'x' variable, its recommended to multiply 'x' variable in both sides of inequality:

we have
`(1)/(4)< x^(2) \\`

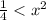
This is a quadratic equation, two answer are going to be obtained from here.

since
`\sqrt{x^(2) } = |x|`

Applying square roots to both sides of inequality sign we wil have the following

`\sqrt{(1)/(4) } < \sqrt{x^(2) }`

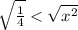
This leaves to the following

`(1)/(4)<|x|`

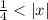
remember that
`|x|= +/ - x`

so

`x>(1)/(2) \\x<(-1)/(2)`