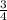Question

Choose the fraction that goes in the blank
7/8 > - > 3/5

Answer 1

The fraction is
`(3)/(4)`

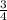
Explanation:

* Lets explain how to solve the problem

- The fraction m/n has m as a numerator and n as a denominator

- To compare between fractions we must to put all of them with

same denominator

- We can make that by find the lowest common multiple (L.C.M) of

the all denominators

- Ex: The L.C.M of the denominators of these fraction

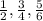`(1)/(2),(3)/(4),(5)/(6)` is 12 because 12 is the first

common multiple of 2 , 4 , 6

- The fractions will be change:

#
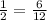`(1)/(2)=(6)/(12)` ⇒ we multiplied up and down by 6

to make the denominator = 12

#
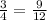`(3)/(4)=(9)/(12)` ⇒ we multiplied up and down by 3

to make the denominator = 12

#
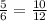`(5)/(6)=(10)/(12)` ⇒ we multiplied up and down by 2

to make the denominator = 12

- The fractions will be
`(6)/(12),(9)/(12),(10)/(12)`

* Lets solve the problem

- To chose a fraction between
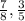`(7)/(8),(3)/(5)`, we must

find The L.C.M for the denominators 8 and 5

∵ The least common multiple of 8 and 5 is 40

∴ The fraction
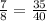`(7)/(8)=(35)/(40)` ⇒ we multiplied up

and down by 5 to make the denominator = 40

∴ The fraction
`(3)/(5)=(24)/(40)` ⇒ we multiplied up

and down by 8 to make the denominator = 40

- Lets find any fraction between
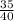`(35)/(40)` and
`(24)/(40)`

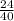
∵ The fraction
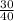`(30)/(40)` is between the fractions

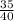`(35)/(40)` and
`(24)/(40)`

∴
`(35)/(40)>(30)/(40)>(24)/(40)`

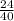
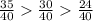
- Lets reduce the fraction to its simplest form

∵ The simplest form of
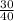`(30)/(40)` is
`(3)/(4)`

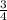
by dividing up and down by 10

∴
`(7)/(8)>(3)/(4)>(3)/(5)`

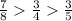
* The fraction is
`(3)/(4)`