Answer:
The exact value of
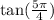 is 1.
is 1.
The reference angle is
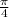
The terminal point is
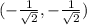 .
.
Explanation:
The given expression is
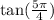
Since
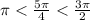 , so it lies in third quadrant.
, so it lies in third quadrant.
We need to find the exact value of given expression.
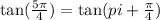
In third quadrant, tangent is positive.
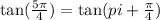
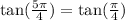
![[\because \tan (\pi+\theta)=\tan \theta]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/onih4ascx64cbociw67gr7bxxtwnoh5nd2.png)

![[\because \tan ((\pi)/(4))=1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/rtjsb5s13nv0a97j1t1p8v3hi3xl70i5b7.png)
Part 1: Reference angle for third quadrant is
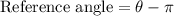
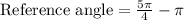
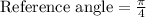
Therefore the reference angle is
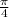 .
.
Part 2: Terminal point associated with the angle be (x,y).
For a unit circle hypotenuse is 1, perpendicular is y and base is x.
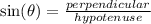

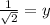

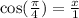
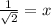
In third quadrant sine and cosine both are negative. So the terminal point is
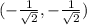 .
.