Question

Determine whether each sum, difference, product,

or quotient represents a rational number or an
irrational number. Explain how you know without
simplifying​

Answer 1

28. The difference represents an irrational number

29. The difference represents a rational number

30. The quotient represents a rational number

31. The quotient represents an irrational number

Explanation:

* Lets explain how to solve the problem

- The rational number is any numbers can be put in the form of a/b,

where a and b are integers b ≠ 0

- Ex: 1 , 2/3 , 5/4 , 22/7 , 100 , ................

- The irrational number is any number that is not rational

- It is a number that cannot be written as a ratio of two integers

or cannot be expressed as a fraction

- Ex: √2 , √7 , π , ..... (π is irrational because it's approximated value)

- If the part of the the number is irrational, then the number

is irrational

- Ex: (5 + √3) , (√7 + 5) , 2√5 , √11/4 , 5/√13

* Lets solve the problems

28.
`(6)/(23)-(√(2))/(2)`

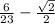
∵ √2/2 is an irrational number

∵ One term is an irrational number

∴ The difference represents an irrational number

29.
`(6)/(23)-(15)/(127)`

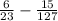
∵ The two terms are rational numbers

∴ The difference represents a rational number

30.
`(6)/(23)` ÷
`(15)/(127)`

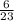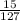
∵ The two terms are rational numbers

∴ The quotient represents a rational number

31.
`(6)/(23)` ÷
`(√(2))/(2)`

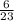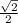
∵ √2/2 is an irrational number

∵ One term is an irrational number

∴ The quotient represents an irrational number