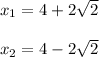Answer:
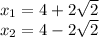
Explanation:
 - 8x+ 8 = 0
- 8x+ 8 = 0
we divide the coefficient of the X by half :
in this case: 8x/2 = 4 , then we do the following
to the result obtained (4) squared: 4^2=16
we sum and subtract by 16 to maintain the balance of equation:
 - 8x+ 16-16+8 = 0
- 8x+ 16-16+8 = 0
we have:
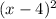 -16 +8=0
-16 +8=0
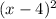 =16-8
=16-8
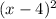 = 8
= 8
we write the square root on both sides of the equation:
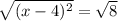
we know:
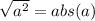
so we have:
abs(x-4)=
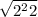
abs(x-4)=2

we have:
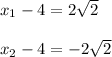
finally we have: