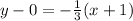Answer:
1.

2.
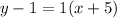
3.

4.
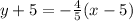
5.
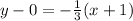
Explanation:
∵ The equation of a line passes through
 and
and
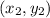 is,
is,
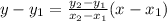
We know that,
The slope of the line is,

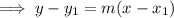
Which is the point slope form of a line,
1. Thus, the equation of line passes through (1, 4) with slope 4 is,

2. The equation of line passes through (-5, 1) and (-4, 2),
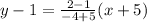
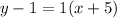
3. The equation of line passes through (-4, 1) and (0, 2),
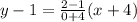

4. Now, two parallel lines having the same slope.
Thus, the slope of line parallel to y = -4/5x - 4 is, -4/5,
So, the equation of line passes through (5, -5) with slope -4/5 is,
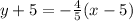
5. If a line has slope m then the slope of perpendicular line is

Slope of line y = x + 3,
Slope of perpendicular line of y = x + 3 = -
 ,
,
So, the equation of line passes through (-1, 0) with slope
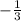 ,
,