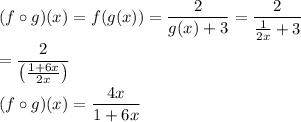Question

Help with 8 and 9??? Please help me out! Correct answers please

Answer 1

8. (-∞, 0) ∪ (0, 1/3) ∪ (1/3, ∞)

9. f(g(x)) = 4x/(1+6x)

Explanation:

8. For f(g(x)) to be defined, g(x) must be defined and f(g(x)) must be defined.

g(x) will be defined for all x≠0. f(g(x)) will be defined for g(x)≠4. Solving g(x)=4, we find the value of x is 1/3. (The answer choices give a clue.)

So, the domain of f(g(x)) is all x that is not 0 or 1/3. Only one answer choice makes those particular exclusions:

(-∞, 0) ∪ (0, 1/3) ∪ (1/3, ∞)

__

9. Substituting the definition of g(x) into the expression for f(x), we get ...

`\displaystyle (f\circ g)(x)=f(g(x))=(2)/(g(x)+3)=(2)/((1)/(2x)+3)\\\\=(2)/(\left((1+6x)/(2x)\right))\\\\(f\circ g)(x)=(4x)/(1+6x)`