Question

Please please helpplpplpol

Answer 1

Answer: -4/5

Explanation:

Ok so cos(x) = -4/5 and we know that:

`sin^2(x) + cos^2(x) = 1`.

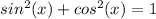If we plug that in and solve for sin(x) we get:

`sin^2(x) = (9)/(25) \\sin(x) = (3)/(5)`

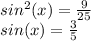
Now we have to consider: is sin(x) positive or negative?

We have that
`\pi  < x < (3\pi )/(2)`.

From the unit circle, we know that sin(x) is negative in this range. Therefore sin(x) actually equals -3/5.

But the question asks: what is
`sin(x + (\pi )/(2))`?

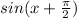Here's where another important equation comes in:

`sin(\alpha  + \beta ) = sin(\alpha)cos(\beta) + cos(\alpha)sin(\beta)`

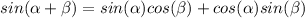
In this case, we have alpha = x and beta = pi/2.

So, that looks like:

sin(x + pi/2 )= sin(x)cos(pi/2) + cos(x)sin(pi/2)

We already have what sin(x) and cos(x) are. We also know that sin( pi/2) = 1 and cos(pi/2) = 0.

sin(x + pi/2 ) = (-3/5)(0) + (-4/5)(1).

Therefore we simply have

sin(x + pi/2) = -4/5