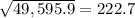Question

Find the variance and standard deviation of the given set of data to the nearest tenth.

{440, 130, 280, 500, 150, 640, 760}


A) variance = 222.7, standard deviation = 49,595.9

B) variance = 49,595.9, standard deviation = 24,798

C) variance = 49,595.9, standard deviation = 222.7

D) variance = 57,861.9, standard deviation = 240.5

Answer 1

Part 1) variance = 49,595.9

Part 2) standard deviation = 222.7

Option C

Explanation:

we have

set of data
`[440,130,280,500,150,640,760]`

step 1

Find the mean

Adds the values and divide by the number of values

In this problem the number of values is 7

`[440+130+280+500+150+640+760]/7`

`[2,900]/7=414.3`

step 2

for each number: subtract the Mean and square the result

`(440-414.3)^(2)=660.49\\ (130-414.3)^(2)= 80,826.49\\ (280-414.3)^(2)= 18,036.49\\ (500-414.3)^(2)= 7,344.49\\ (150-414.3)^(2)= 69,854.49\\ (640-414.3)^(2)= 50,940.49\\ (760-414.3)^(2)=119,508.49`

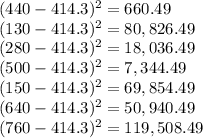
step 3

work out the mean of those squared differences

`[660.49+80,826.49+18,036.49+7,344.49+69,854.49+50,940.49+119,508.49]/7=347,171.43/7=49,595.9` ----> this value is called the "Variance"

step 4

The standard deviation is the square root of the variance

so

The standard deviation is equal to

`√(49,595.9)=222.7`