Question

The area of a rectangle is represented by the function x3 − 3x2 − 40x + 84. The width of the rectangle is x − 7. Find the expression representing the length of the rectangle.

x2 + 4x − 12
x2 + 8x + 12
x2 + 2x − 24
x2 + 10x + 14

Answer 1

a is the answer x^2+4x-12

Answer 2

For this case we have that by definition, the area of a rectangle is given by:

`A = w * l`

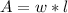
Where:

w: It is the width

l: It is the length

According to the data we have to:

`A = x ^ 3-3x ^ 2-40x + 84\\w = x-7`

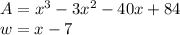
Then l = \ frac {x ^ 3-3x ^ 2-40x + 84} {x-7}

According to the attached figure we have that the quotient is
`x ^ 2 + 4x-12`

So, the length is
`l = x ^ 2 + 4x-12`

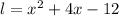
Answer:

Option A