Question

A Carnot air conditioner takes energy from the thermal energy of a room at 63°F and transfers it as heat to the outdoors, which is at 100°F. For each joule of electric energy required to operate the air conditioner, how many joules are removed from the room?

Answer 1

For the Carnot air conditioner working as a heat pump between 63 and 100°F , It would transfer 3.125 Joules of heat for each Joule of electric energy supplied.

Step-by-step explanation:

The process described corresponds to a Carnot Heat Pump. A heat pump is a devices that moves heat from a low temperature source to a relative high temperature destination. To accomplish this it requires to supply external work.

For any heat pump, the coefficient of performance is a relationship between the heat that is moving to the work that is required to spend doing it.

For a Carnot Heat pump, its coefficient of performance is defined as:

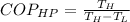`COP_(HP)=(T_H)/(T_H-T_L)` Where:

• T is the temperature of each heat deposit.

• The subscript H refers to the high temperature sink(in this case the outdoors at 100°F)

• The subscript L refers to the low temperature source (the room at 63°F)

Then, for this Carnot heat pump:

`COP_(HP)=(T_H)/(T_H-T_L)=(100°F)/(100°F-63°F)=3.125`

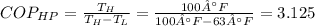
So for each 3.125 Joules of heat to moved is is required to supply 1 Joule of work.