Question

Use the following information to determine your answers: The typical amount of sleep per night that adults get has a bell-shaped distribution with a mean of 7.5 hours and a standard deviation of 1.3 hours. Suppose last night you slept for 5 hours. How many standard deviations are you from the mean

Answer 1

Approximately 1.9 standard deviation below mean.

Explanation:

We have been given that the typical amount of sleep per night that adults get has a bell-shaped distribution with a mean of 7.5 hours and a standard deviation of 1.3 hours. Last night you slept for 5 hours.

We will use z-score formula to solve our given problem as z-score tells that a data point is how many standard deviation above or below mean.

`z=(x-\mu)/(\sigma)`, where,

z = z-score,

x = Sample score,

`\mu` = Mean,

`\sigma` = Standard deviation.

`z=(5-7.5)/(1.3)`

`z=(-2.5)/(1.3)`

`z=-1.92307`

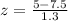
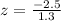
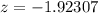
Therefore, you are approximately 1.9 standard deviation below mean.