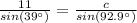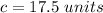Answer:
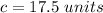
Explanation:
step 1
Find the measure of angle B
Applying the law of sines
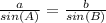
substitute the given values
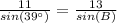
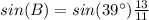
![B=arcsin[sin(39\°)(13)/(11)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/5wwpkgesq1gzpwm6qh9onm7bzxn1ur845y.png)
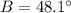
step 2
Find the measure of angle C
Remember that the sum of the interior angles of a triangle must be equal to 180 degrees
so
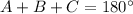
substitute the given values
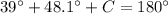
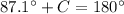
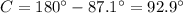
step 3
Find the length side of c
Applying the law of sines
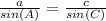
substitute the given values