Question

The local oil changing business is very busy on Saturday mornings and is considering expanding. A national study of similar businesses reported the mean number of customers waiting to have their oil changed on Saturday morning is 3.6. Suppose the local oil changing business owner wants to perform a hypothesis test. The null hypothesis is the population mean is 3.6 and the alternative hypothesis that the population mean is not equal to 3.6. The owner took a random sample of 16 Saturday mornings during the past year and determined the sample mean is 4.2 and the sample standard deviation is 1.4. It can be assumed that the population is normally distributed and the level of significance is 0.05. The critical t value for this problem is _______.

Answer 1

2.131

Explanation:

Given : Sample size = 16

Sample mean is 4.2

Sample standard deviation is 1.4.

Level of significance is 0.05.

To Find : critical t value

Solution:

Sample size = 16

Since n < 30

So we will use t - test

We are supposed to find critical t value

Degree of freedom = n-1 = 16-1 = 15

Level of significance =α= 0.05

Now refer the t table for t critical

`t_({(\alpha)/(2),d.f.})` =
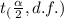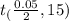`t_({(0.05)/(2),15})` = 2.131

Hence The critical t value for this problem is 2.131