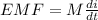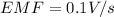Answer:
Part a)
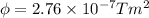
Part B)
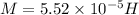
Part C)
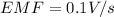
Step-by-step explanation:
Part a)
Magnetic field due to a long ideal solenoid is given by

n = number of turns per unit length
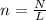
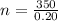
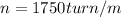
now we know that magnetic field due to solenoid is
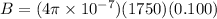
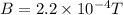
Now magnetic flux due to this magnetic field is given by
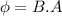
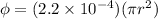
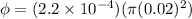
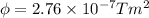
Part B)
Now for mutual inductance we know that
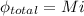
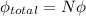
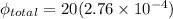
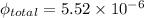
now we have
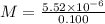
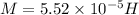
Part C)
As we know that induced EMF is given as