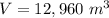Question

A room is 30m long , 24m broad and 18m high. Find (a) Length of the longest rod that can be placed in the room. (b) Its tolal surface area. (c) Its volume

Answer 1

Part a) The length of the longest rod that can be placed in the room is 42.43 m

Part b) The total surface area is
`SA=3,384\ m^2`

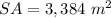
Part c) The volume is equal to
`V=12,960\ m^3`

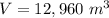
Explanation:

Part a) Find the length of the longest rod that can be placed in the room

The room is in the shape of a rectangular prism, so the longest rod that can be placed in the room is equal to the diagonal of the rectangular prism

Let

d -----> diagonal of the base of the room

D ----> diagonal of the rectangular prism

step 1

Find the diagonal of the base

Applying the Pythagoras Theorem

`d^(2)=30^(2)+24^(2)`

`d^(2)=1,476`

`d=√(1,476)\ m`

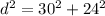
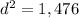
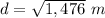
step 2

Find the diagonal of the rectangular prism

The legs of the diagonal of the rectangular prism are the diagonal of the base and the height of the room

Applying the Pythagoras Theorem

`D^(2)=(√(1,476))^(2)+18^(2)`

`D^(2)=1,476+324`

`D^(2)=1,800`

`D=42.43}\ m`

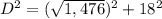
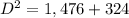
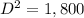
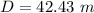
Part b) Find the total surface area

we know that

The total surface area of the room is equal to

`SA=2B+PH`

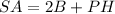
where

B is the area of the base of the room

P is the perimeter of the base of the room

H is the height of the room

so

`SA=2[(30)(24)]+2[30+24](18)`

`SA=1,440+1,944`

`SA=3,384\ m^2`

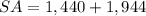
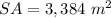
Part c) Find the volume

we know that

The volume of the room is equal to

`V=BH`

where

B is the area of the base of the room

H is the height of the room

so

`V=[(30)(24)](18)`

`V=12,960\ m^3`