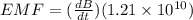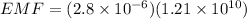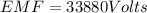Answer:
Step-by-step explanation:
As per Faraday's law of Electromagnetic induction we know that
Rate of change in magnetic flux will induce EMF in the closed conducting loop
so we have
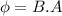
now we have
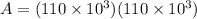
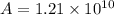
now we have
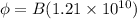
now the induced EMF through this loop is given as