Question

Two fair dice, one blue and one red, are tossed, and the up face on each die is recorded. Define the following events:

E: {The difference of the numbers is 3 or more}
F: {The numbers are equal}

Find the following probabilities:
(a) P(E)= _____
(b) P(F)= _____
(c) P(EF) = _____

Answer 1

(a)
`(1)/(3)`

(b)
`(1)/(6)`

(c) 0

Explanation:

After tossing two dice, the possible events may be as per following table.

Die - 1

1 2 3 4 5 6

Die 2

1 1,1 1,2 1,3 1,4 1,5 1,6

2 2,1 2,2 2.3 2,4 2,5 2,6

3 3,1 3,2 3,3 3,4 3,5 3,6

4 4,1 4,2 4,3 4,4 4,5 4,6

5 5,1 5,2 5,3 5,4 5,5 5,6

6 6,1 6,2 6,3 6,4 6,5 6,6

E : (1,4), (1,5), (1,6), (2,5), (2,6), (3,6), (4,1), (5,1) (5,2), (6,1), (6,2), (6,3)

(a) P(E) =
`\frac{\text{favorable events}}{\text{total events}}`

=
`(12)/(36)`

=
`(1)/(3)`

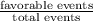
F : (1,1), (2,2), (3,3), (4,4), (5,5), (6,6)

(b) P(F) =
`(6)/(36)`

=
`(1)/(6)`

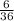
(c) P(EF) = 0

Even a single event is not common in E and F. Therefore, P(EF) would be 0.

Answer 2

Explanation:

Given that two fair dice, one blue and one red, are tossed, and the up face on each die is recorded.

a) P(E) = P(the difference of the numbers is 3 or more}

Favourable events are (1,4) (1,5)(1,6) (2,5) (2,6) (3,6) (4,1) (5,1) (5,2) (6,1) (6,2)(6,3)

P(E) =
`(12)/(36) =(1)/(3)`

b)P(F)

Favourable events for F = (1,1) (2,2)...(6,6)

P(F) =
`(6)/(36) =(1)/(6)`

c) P(EF)

There is no common element between E and F

P(EF) =0