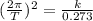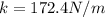Answer:
Part a)

Part b)
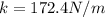
Step-by-step explanation:
Here we know that
Amplitude = 5.55 cm
Time period = 0.250 s
mass = 0.273 kg
Part a)
As we know that an object is executing SHM so the maximum acceleration of SHM is given as
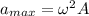
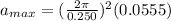

now we know that
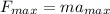
here we have

Part b)
We know that angular frequency of SHM is given by following formula when it is a spring block system
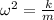
so here we have