Answer:
0.1507 or 15.07%.
Explanation:
We have been given that the manufacturing of a ball bearing is normally distributed with a mean diameter of 22 millimeters and a standard deviation of .016 millimeters. To be acceptable the diameter needs to be between 21.97 and 22.03 millimeters.
First of all, we will find z-scores for data points using z-score formula.
 , where,
, where,
z = z-score,
x = Sample score,
 = Mean,
= Mean,
 = Standard deviation.
= Standard deviation.
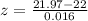
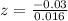
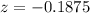
Let us find z-score of data point 22.03.
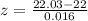
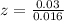

Using probability formula
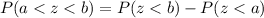 , we will get:
, we will get:
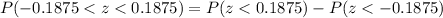
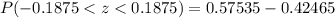
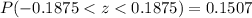
Therefore, the probability that a randomly selected ball bearing will be acceptable is 0.1507 or 15.07%.