Answer:
The force exerted by the biceps muscle is 1485.58 N.
Step-by-step explanation:
Given that,
Length = 0.445 m
Mass of forearm = 2.15 cm
Mass of the object = 6.15
Distance = 2.15 cm
We need to calculate the force exerted by the biceps muscle
Under the equilibrium condition
Moment about E = 0
Using free body diagram of muscle
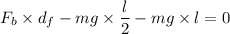
Where,
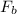 = force by biceps
= force by biceps
put the value into the formula


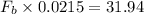
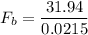

Hence, The force exerted by the biceps muscle is 1485.58 N.