Question

The amount of ketchup dispensed into a container follows a normal distribution with a mean of 16 ounces and a standard deviation of 0.2 ounce. A sample of 25 containers revealed a mean fill of 16.04 ounces. Is the sample mean significantly different from 16 ounces? Use the 0.05 significance level.

Answer 1

Answer: Yes, the sample mean is significantly different from 16 ounces.

Explanation:

Since we have given that

`H_0:\mu =16\\\\H_1:\mu\\eq 16`

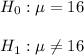
Mean = 16 ounces

Standard deviation = 0.2 ounces

`\bar{X}=16.04`

Number of containers = 25

Since there are 25 containers i.e. n = 25

n<30.

so, we will do t-test.

Using the normal distribution, we get that

`z=\frac{\bar{X}-\mu}{(\sigma)/(√(n))}\\\\t=(16.04-16)/((0.2)/(√(25)))\\\\t=(0.04* 5)/(0.2)\\\\z=1`

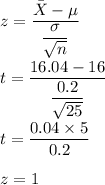
Here, degree of freedom v = n-1 = 25-1 = 24

So,
`t_(\alpha,v)=t_(0.05,24)=1.711`

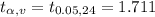
Since we can check that

`1<1.711`

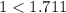
So, we will reject the null hypothesis.

Hence, Yes, the sample mean is significantly different from 16 ounces.