Question

suppose that incomes of families in Newport Harbor are normally distributed with a mean of $750,000 and a standard deviation of $250,000. If 4 families are selected at random from this community, what is the probability that their combined income is exceed $4 million. What is the probability that the average income of these 4 families exceeds $800,000?

Answer 1

Answer: 0.345

Explanation:

Given : The incomes of families in Newport Harbor are normally distributed with Mean :
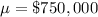`\mu=\$ 750,000` and Standard deviation :
`\sigma= $250,000`

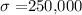
Samples size : n=4

Let x be the random variable that represents the incomes of families in Newport Harbor.

The z-statistic :-

`z=(x-\mu)/((\sigma)/(√(n)))`

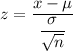
For x= $800,000

`z=(800000-750000)/((250000)/(√(4)))=0.4`

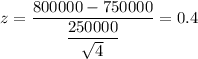
By using the standard normal distribution table , we have

The probability that the average income of these 4 families exceeds $800,000 :-

`P(x>80,000)=P(z>0.4)=1-P(z\leq0.4)\\\\=1-0.6554217=0.3445783\approx0.345`

Hence, the probability that the average income of these 4 families exceeds $800,000 =0.345