Question

Refer to the Scheer Industries example in Section 8.2. Use 6.84 days as a planning value for the population standard deviation. a. Assuming 95% confidence, what sample size would be required to obtain a margin of error of 1.5 days (to the nearest whole number)? b. Assuming 90% confidence, what sample size would be required to obtain a margin of error of 2 days (to the nearest whole number)?

Answer 1

Answer: a) 80 b) 32

Explanation:

a) Given : Significance level :
`\alpha=1-0.95=0.05`

Critical value :
`z_(\alpha/2)=1.96`

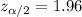
Standard deviation : s =6.84

Margin of error : E= 1.5

The formula to find the sample size is given by :-

`n=((z_(\alpha/2)\ \sigma)/(E))^2`

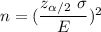
i.e.
`n=(((1.96)(6.84))/(1.5))^2=79.88069376\approx80`

Hence, the required minimum sample size = 80

b) Given : Significance level :
`\alpha=1-0.90=0.10`

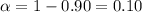
Critical value :
`z_(\alpha/2)=1.645`

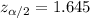
Standard deviation : s =6.84

Margin of error : E= 2

The formula to find the sample size is given by :-

`n=((z_(\alpha/2)\ \sigma)/(E))^2`

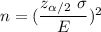
i.e.
`n=(((1.645)(6.84))/(2))^2=31.65075081\32`

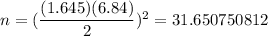
Hence, the required minimum sample size =32