Answer:
36 gallons of each first brand and 24 gallons second brand of antifreeze must be used.
Step-by-step explanation:
Let the volume of two different antifreeze be x and y.
Total volume required = 60 gal
x + y = 60 gal ...(1)
In order to obtain 60 gallons of a mixture that contains 45% pure antifreeze.
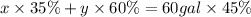
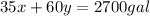
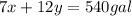
On solving equation (1) ans (2), we get:
x = 36 gal, y = 24 gal
36 gallons of each first brand and 24 gallons second brand of antifreeze must be used.